前言

随着风力发电、石油化工、核电工程、船舶制造、矿业冶金以及交通设施等建设步伐的加快，国内对干吨级起重机的需求表现得越来越迫切。近几年，国内相关企业开始开展千吨位级全地面起重机的国产化研制工作。转盘轴承是全地面起重机回转机构的关键部件，其结构形式较为特殊，受力情况十分复杂。由于受到径向空间的限制，该转盘轴承采用六排圆柱滚子的结构形式，以期在有限的径向尺寸范围内通过增加滚子的排数来保证所需的承载能力。

在起重机安全监控管理系统工作时，转盘轴承主要承受倾覆力矩和轴向载荷作用。干吨级全地面起重机作为一种高端装备对转盘轴承的可靠性要求极高。全地面起重机用转盘轴承合理设计和正确选型是建立在对其进行系统的力学分析的基础之上的。目前，对转盘轴承力学性能的研究引起了国内外研究人员的极大兴趣。ZUPAN和PREBILm建立了单排四点接触球转盘轴承的静力学平衡方程组，分析了轴承的承载能力与接触几何参数之间的关系。SMOLNICKI和RUSINSKITM建立了基于超单元的离散转盘轴承有限元模型，超单元表示“滚道．滚动体．滚道”之间的作用，用这个模型分析了双排球转盘轴承支撑结构的变形和柔性不均匀性对滚动体载荷影响。POTOt兰NIK等p1采用矢量来表示双排四点接触球转盘轴承的几何结构，并建立了轴承的静力学平衡方程组，求解得到最大滚动体载荷，并对滚动体与滚道之间的接触进行了有限元分析。李云峰H建立了单排四点接触转盘轴承的承载能力曲面，并利用该曲面分析了游隙、沟曲率半径系数、接触角等参数的改变对转盘轴承承载能力的影响规律。高学海等p1研究了双排四点接触球转盘轴承的滚道接触压力分布规律，分析了几何参数对转盘轴承承载能力的影响。

CHEN掣刨建立了双排四点接触球转盘轴承的数值计算模型，分析了轴承的几何参数对轴承承载能力的影响。王燕霜掣¨研究了特大型双排四点接触球轴承承载曲线的精确计算方法，并分析了转盘轴承参数对承载能力的影响规律。GONCZ等婵1建立了三排滚子转盘轴承的简化有限元模型，计算得到了滚动体的载荷分布，并分析了滚子凸度对接触应力的影响。于春来等p1利用滚动体载荷分布系数和载荷分布积分系数建立了三排滚子转盘轴承的平衡力学模型，利用轴向载荷与倾覆力矩载荷之间的比值关系查表得到两个系数的值，并进一步计算得到滚动体载荷分布和转盘轴承的寿命。转盘轴承的承载能力是判断其能否满足主机使用要求的关键指标。现有有关滚子转盘轴承的力学计算模型未能包含包括游隙在内的多个重要设计参数，未能考虑这些参数对转盘轴承承载能力的影响，不便于根据分析结果对转盘轴承的设计参数进行优化。

本文的目的是针对l 200 t全地面起重机用六排滚子转盘轴承，通过建立包含包括游隙在内的全部设计参数的力学模型，系统地分析承受轴向载荷和倾覆力矩的联合载荷作用的转盘轴承的内部载荷分布，在此基础上计算出转盘轴承的承载能力，并分析影响承载能力的相关因素。

1、轴承力学系统建模

1．1变形协调条件全地面起重机用六排滚子转盘轴承的结构如图1所示，主要由内圈、外圈、中圈以及六排滚子所构成的。转盘轴承的内圈和外圈安装在主机机身的安装平台上固定不动，中圈与起重机的吊臂支座相联。起重机起吊作业时，转盘轴承承受被起吊重物所造成的轴向载荷和倾覆力矩的联合作用。在外部载荷的作用下，转盘轴承的中圈相对于固定的内圈和外圈产生相对位移。在分析时，假定在外部轴向载荷疋和倾覆力矩载荷M的共同作用下，中圈产生的相应的轴向位移和倾角位移分别为皖和0。为便于定义每一个滚子在转盘轴承圆周上的位置，以转盘轴承的中心为坐标原点，在转盘轴承的径向平面内建立一个极坐标系，坐标系的极轴通过受载最大的滚子的轴线。在轴承的径向平面内建立坐标系如图2所示，极角用y表示。则对六排滚子中的任一排滚子来说，每个滚子的位置角可以表示为在转盘轴承的中圈产生位移皖和p后，与每一个滚子相接触作用的两滚道面之间的法向距离将发生变化，也就是将产生沿接触法向的趋近量，如图3所示。从图中可以看出，在每一个滚子位置少，由于中圈位移所造成的法向趋近量是由两部分组成的：其一是中圈的轴向位移产生的，等于皖；其二1是中圈的倾角位移产生的，等于妄矗-口·COSg／

1．2算法及程序正确性的验证为验证本文算法及计算程序的正确性，本文针对1 200 t全地面起重机用六排滚子转盘轴承进行了计算，并与ANSYS软件的计算结果进行了对比。六排滚子转盘轴承的主参数如表1所示，所承受的外部载荷为：Fo=6 680 kN，M=9 470 kN·m。在对转盘轴承装配体进行有限元分析时，采用“实体单元．弹簧单元”混合模型。将滚子简化为弹簧单元COMBIN39，套圈采用四面体单元SOLID92，混合有限元模型如图4所示。考虑到转盘轴承的内圈和外圈与主机机身相联固定不动，内圈和外圈的下底面与安装平台相接触，所以，对转盘轴承的内圈和外圈下底面施加全自由度约束。转盘轴承的工作载荷通过起重机吊臂作用到中圈的上端面上。为便于轴向载荷和倾覆力矩载荷的施加，在中圈上端面的中心处建立一个加载辅助节点，并用质量单元MASS21对其划分网格，然后，将辅助节点与内圈上端面的所有节点耦合起来构成一个刚性区域。最后，在辅助节点上分别施加轴向载荷和倾覆力矩载荷，加载及边界条件设置如图5所示。

通过对转盘轴承整体有限元模型的求解计算得到每个滚子所承受的载荷，将该结果与本文算法得到的结果进行比较，如图6所示。从图中所示的计算结果可以看出，本文算法的计算结果与有限元分析软件ANSYS的计算结果基本一致。有限元法将套圈看成弹性体，在轴承受到外部载荷作用时套圈上的悬伸滚道结构发生轴向平面内的结构变形，使得计算结果与本文方法得到的结果在数值上有所差别。另外，采用有限元法得到的结果曲线的局部波动归因于该方法将轴承套圈离散为有限个单元，当求解计算满足收敛所设定的阈值时计算结束，曲线上各点的数值为计算结束时所调整到的值。通过这些结果的对比验证了本文算法及计算程序的正确性。2分析与讨论在起重机作业时，转盘轴承做重载低速回转运动。在转盘轴承内部滚子与滚道接触部位，过大的接触应力作用将会造成的滚道面的永久塑性变形，这将会影响到转盘轴承的工作性能并可能出现过早失效。根据沈伟毅等uu的试验结果，转盘轴承的滚子与滚道之间接触应力I仃I应当限制在3 300 MPa，这一应力值被用作滚子与滚道之间的许用接触应力。

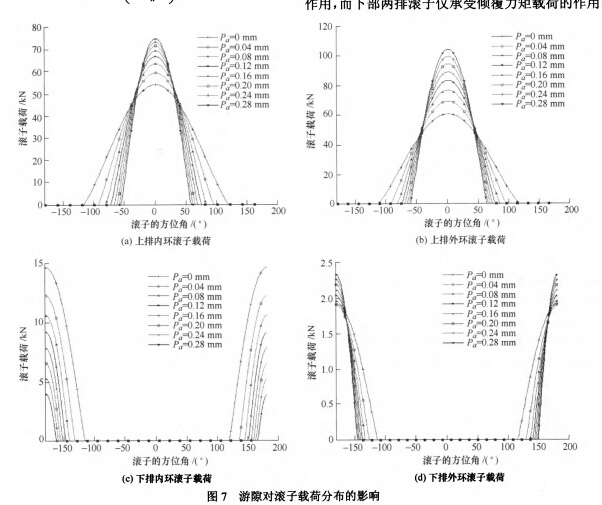
根据Hertz接触理论，可以得到滚子与滚道之间接触应力的计算公式式中 Q——滚子载荷；乏：P——滚子与滚道接触线的主曲率和函数；L——滚子的长度。在转盘轴承中每个滚子所受的载荷是不同的，考虑受载最大的滚子，由其载荷Q。计算出该滚子与滚道之间接触应力‰。再由‰；计算转盘轴承的承载能力安全系数工_(埘 ∞，安全系数Z是衡量转盘轴承的承载能力的主要性能指标，对该指标的计算是建立在对转盘轴承进行整体力学分析的基础之上的。根据1 200 t全地面起重机用转盘轴承的工况条件和设计参数，利用本文的力学模型进行了转盘轴承的分析计算。首先，通过对方程式(10)、(11)的求解得到中圈位移将皖和秒的；然后，利用式(4)、(5)、(8)、(9)计算得到所有的滚子载荷。图7为对应于不同的轴承轴向游隙时，沿轴承圆周方向分布的所有滚子载荷。从图中可以看出，轴承上部两排滚子的载荷显著大于下部两排滚子的载荷，这是因为上部两排滚子同时承受轴向载荷和倾覆力矩载荷的作用，而下部两排滚子仅承受倾覆力矩载荷的作用；另外，外环滚子的载荷大于内环滚子的载荷，这是因为外环滚子距离轴承中心更远，在中圈产生倾角位移时，外环滚道面弹性趋近量大于内环滚道，相应的外环滚子也具有更大的弹性接触变形量。根据计算得到的最大滚子载荷，利用式02)、(13)可以计算得到轴承的安全系数。图8所示为转盘轴承的安全系数随轴承游隙的变化情况，图中曲线表明了轴承的轴向游隙对其承载能力的影响规律。可以从图中看出，在轴向游隙从0 mnl增大到0．28 lnnl的过程中，轴承的承载能力先是随之快速下降，然后再缓慢下降。

这可以被归结为两方面的原因：其一，随着轴向游隙从0 mm到0．28衄的增大，承担轴承外部载荷的滚子数量越来越少，最大滚子载荷也随时增加，相应的载荷安全系数也随之减小。当轴向游隙为0 rain时轴承的安全系数是2．66，然而，当轴向游隙增加到0．28 Illnl时，轴承’的安全系数仅为1．54，也就是安全系数下降了42％。所以，在工程实际中，转盘轴承的实际安全系数比对应于0 mill游隙的名义安全系数小很多

2 结论

(1)建立了千吨级全地面起重机用六排滚子转盘轴承的力学模型，通过与有限元模型计算结果的比较，验证了力学模型的正确性。

(2)转盘轴承上部两排滚子的载荷显著大于下部两排滚子的载荷，上排外环滚子的载荷大于上排内环滚子的载荷，下排外环滚子的载荷大于下排内环滚子的载荷。

(3)随着轴向游隙的增大，轴承内部承担载荷的滚子数量逐渐减少，受载最大的滚子载荷也逐渐增大，这一趋势在游隙增大的初期更加明显。

(4)在转盘轴承的轴向游隙从0 i／lnl增大到0．28 mill的过程中，轴承的承载能力先是随之快速下降，然后再缓慢下降。当轴向游隙增加到0．28 nllTl时，轴承的安全系数下降了42％。