摘要：以某库房32tXl6．5m桥式起重机为研究对象，提出了一种基于在线监测系统获取全程应力谱的新方法。在此基础上，结合材料的P-S．N曲线，考虑疲劳极限的模糊性，利用模糊累积损伤理论对主梁进行了疲劳寿命估算。结果表明：该桥式起重机主梁的剩余疲劳寿命为38．8年，为起重机的长期安全使用和后期维修提供可靠依据。‘

0前言

由于实际工况与预期工况存在较大的差异，桥式起重机的实际寿命通常会偏离其设计寿命。若根据起重机在线监测系统寿命对起重机进行大修或报废，将出现浪费和危险并存的问题。因此，根据实际工况对桥式起重机进行寿命预测，可以为起重机的维修和报废提供可靠依据，具有重要的工程意义和经济价值。

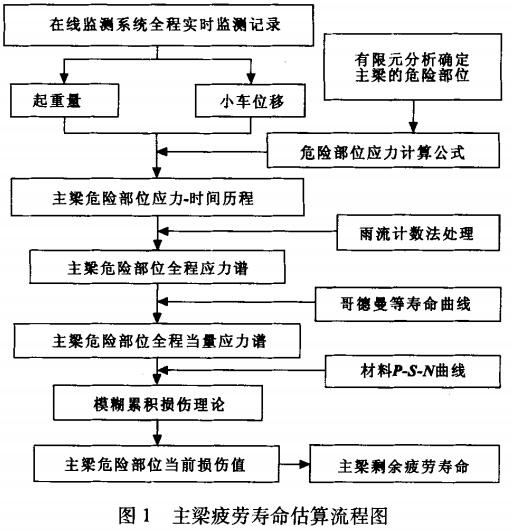
起重机的实际工况主要由应力谱反映，因此应力谱的获取是预测起重机实际寿命的关键。目前，常用的应力谱获取方法有现场实测法和计算机仿真法，这两种方法是通过实测或仿真获取采样时间内的应力谱。随着经济的快速发展，起重机的使用量和工作强度呈持续增大的趋势，因此，采样时间内的应力谱与历史应力谱和未来的应力谱有明显差异，仅根据采样时问内的应力谱进行全寿命预测存在较大失真。针对这两种方法的不足，本文作者基于在起重机安全监测系统，全程实时监测反映起重机实际工况的相关参数，通过对监测数据的计算和处理，获取起重机自服役至今的全程应力谱，该应力谱准确反映了起重机的全程实际使用工况。主梁疲劳寿命基本决定了整机寿命，因此，基于全程应力谱，利用模糊累积损伤理论对主梁疲劳寿命进行估算，流程如图1所示。

1、主梁危险部位的确定

主梁的疲劳破坏多发于应力集中和形变较大的危险部位，因此通常基于危险部位的应力谱进行疲劳寿命估算。文中以某库房32 t×16．5 in桥式起重机为研究对象，在满载小车位于跨中的工况下，通过对主梁进行有限元分析确定其危险部位。

1．1模型的建立

利用3D绘图软件Pro／E建立主梁三维模型(见图2)。

图2主梁Pro／E三维模型将主梁的Pro／E三维模型导入有限元分析软件ANSYS Workbench，进行网格的划分(见图3)。

1．2材料特性、约束与载荷的添加

主梁材料为Q235．B，弹性模量E=210GPa，泊松比肛=0．3，密度P=7．85×10“kg／mm3。由于防爆电控箱和大车运行机构安装在走台侧主梁上，因而走台侧主梁比另一侧主梁承受更大的载荷，故以走台侧主梁为研究对象。因建模时对主梁结构做了必要的简化，导致所建模型的质量小于主梁的实际质量，为此采用密度补偿法，将电气系统、运行机构和走台的总质量(6．734 t)附加在主梁自重(6．216 t)上，因此材料密度设置为1．648x 10。kg／mm3。

主梁两端焊接在端梁上，故约束主梁两端的所有自由度。将小车自重(8．325t)和起重量(32t)平均分配给4个车轮，按力载荷(98 796N)施加在轨道与车轮的接触线上；主梁、电气系统、大车运行机构及走台的质量，按重力加速度的惯性载荷进行施加。

1．3分析结果

对主梁进行有限元分析，得到应力与形变分布云图(见图4)。由图4可知，跨中下盖板既存在应力集中又有最大形变，又考虑到焊缝疲劳强度较弱，因此起重机在线监测系统可以确定主梁最危险的部位为跨中下盖板与腹板的焊缝。

2基于在线监测系统获取应力谱

2．1危险部位的应力计算

根据弯曲正应力公式，计算主梁跨中下盖板与腹板焊缝处的应力

盯2：—掣一 (1)LJ

l

』：

式中：M为主梁跨中的弯矩；

Y为危险部位到跨中截面中性轴。的距离；t为跨中截面对中性轴的惯性矩。当小车位移戈的大小范围不同时，主梁跨中弯矩M有不同计算公式，分别为：

(1)当算<÷一f=3 345 mm，即小车两车轮均位于跨中左侧时，则M=丁GIL+竽∽丢) (2)

式中：G．为主梁、电气系统、大车运行机构及走台的总质量；

G，为小车自重；G为起重量；戈为小车位移，小车位于最左侧时，菇=0；￡为跨度；2为小车轮距。

(2)当3 345 mm≤石≤÷=5 000 mln，即跨中在小车两车轮之间时，则M：了GIL+竿(h4 一÷) (4)、7

、 7

8 2

2．2在线监测系统由式(1)一(4)可知，危险部位的应力随起质量G和小车位移戈的变化而变化。因此，设计在起重机在线监测系统全程实时监测起重量和小车位移，根据式(1)一(4)对监测数据进行计算，可得到起重机自服役至今的应力一时间历程。起重量和小车位移的监测原理如下：

(I)起重量的监测：将压力传感器安装在卷筒的轴承座下(见图5)

(2)小车位移的监测：将绝对值型旋转光电编码器安装在小车的车轮轴上(见图6)，测出车轮角位移o，再根据式(6)可计算得到小车位移z。 (6)戈=OxR式中：R为小车的车轮半径。

2．3全程当量应力谱

利用雨流计数法处理应力一时间历程，可获取反映起重机自服役至今实际使用工况的全程应力谱。由于S—N曲线通常是在均值为0的对称循环载荷作用下获取的，而主梁承受的是随机载荷，产生的应力谱均值不为0，所以需要将全程应力谱转换为均值为0

根据等寿命曲线，可将平均值为盯。的循环应力，转换为平均值为0的等效循环应力，等效循环应力的幅值q为G=2NxF (5) 式中：盯。为材料的抗拉强度根据式(7)，可将全程应力谱转换为均值为。

式中：Ⅳ为起重倍率。

3模糊累积损伤理论

目前，工程上主要利用Miner线性累积损伤理论估算构件的疲劳寿命，但该方法认为：以疲劳极限为为界，大于疲劳极限的应力能对构件产生损伤，小于疲劳极限的应力不能对构件产生损伤。事实上，构件的疲劳极限具有“不确定性”，疲劳极限附近的应力能否对构件产生损伤存在模糊性，不能绝对地将疲劳极限作为应力能否对构件产生损伤的界线。因此，需要考虑疲劳极限的模糊性，根据模糊理论对Miner线性累积损伤理论进行修正。

描述疲劳极限模糊性的关键是建立隶属函数，文献[3]通过实例验证了以升半正态分布为隶属函数进行计算时，疲劳寿命的误差最小。因此，以升半正态分布为隶属函数，计算应力对主梁危险部位产生损伤的概率。隶属函数的曲线如图8所示，表达式为。

(2)小车位移的监测：将绝对值型旋转光电编

码器安装在小车的车轮轴上(见图6)，测出车轮角位移o，再根据式(6)可计算得到小车位移z。 式中：R为小车的车轮半径。

4结论

(1)提出了一种基于在线监测系统的监测数据，通过计算处理，获取全程应力谱的新方法，该全程应力谱能真实地反映起重机自服役至今的实际使用工况，保证了主梁剩余疲劳寿命估算的准确性，为桥式起重机的寿命预测提供了新思路。

(2)考虑疲劳极限的模糊性，起重机在线监测系统建立隶属函数对线性累积损伤理论进行了修正，使主梁的疲劳寿命估算更加符合实际情况。

(3)基于全程应力谱，结合材料的P—S—N曲线，利用模糊累积损伤理论估算出某库房32txl6．5m桥式起重机主梁的剩余疲劳寿命为38．8年，为起重机的长期安全使用和后期维修提供可靠依据。